[NLP] Word Embedding, Word2Vec

1. Vector Representation

자연어를 컴퓨터가 이해하고 학습할 수 있도록 적절하게 숫자로 변형해주는 과정이 필요하다. vector representation은 텍스트를 벡터로 표현하는 방법으로 텍스트를 벡터공간 상의 점으로 표시한다. vector로 표현하는 것의 목적은 의미가 비슷한 텍스트는 공간 상 거리가 가깝도록 하고 의미가 다른 단어는 벡터 공간 상 거리가 멀도록 표현하는 것에 있다. 이를 통해 비슷한 단어들끼리 뭉쳐있도록 하는 역할을 한다고 볼 수 있다(거리를 통해 단어간 유사도를 구하는 방법이라고도 볼 수 있다.) 단어를 벡터로 표현하고 위해서는 주어진 텍스트를 단어 단위로 쪼개고 vocabulary(단어 집합)를 만드는 전처리 과정이 필요하다. 본 글에서는 전처리 과정이 모두 끝났다고 가정하고 단어를 벡터로 표현하는 방법에 대해 이야기하고자한다.

Sparse Representation

단어를 벡터로 표현하는 방법으로 단어 집합의 크기와 동일한 차원의 벡터를 만드는 방법이 있다. 단어 집합 크기와 동일한 차원의 벡터를 통해 표현하고자 하는 단어의 인덱스는 1로 하고 나머지 단어들의 인덱스를 0으로 표시한다. 이렇게 표현하는 방식을 one-hot vector(원-핫 벡터)라고 한다.

벡터와 행렬에서 대부분의 값이 0인 것을 sparse 하다고 한다. one-hot vector는 표현하고자 하는 단어 외에 모든 단어들을 0으로 표시하기 때문에 sparse 하다고 할 수 있다. 이러한 표현 방식을 sparse representation이라고 한다.

sparse representation은 대부분의 값이 0으로 채워져있기 때문에 컴퓨터로 표현할 때 공간적 낭비가 심하다. 실질적으로 의미를 가지는 값이 적고 큰 의미가 없는 값들이 메모리 공간을 많이 차지하기 때문에 공간 상의 낭비와 메모리 소모를 불러 일으킨다.

one-hot vector도 sparse representation이기 때문에 마찬가지로 위와 같은 단점이 존재한다. 특히 one-hot vector는 하나의 값만 1을 가지고 나머지 값은 0을 가지기 때문에 공간적 낭비가 더 심하다고 할 수 있다. 앞서 단어를 벡터를 표현하고자 하는 것의 목적이 비슷한 단어들 간의 거리가 가깝도록 하는 것인데 one-hot vector로 표현을 하게 되면 모든 단어 벡터간의 거리가 $\sqrt{2}$로 동일하기 때문에 목적에도 잘 맞지 않는다는 것을 알 수 있다.

Dense Representation

sparse represenation과 반대로 대부분의 값이 0이 아닌 표현 방식이다. dense representation은 벡터의 차원을 집합의 크기로 설정하지 않기 때문에 sparse representation보다 공간적 낭비도 덜 하다는 장점도 존재한다. 대신 단어를 dense representation으로 표현하기 위해서 별도의 학습 과정이 필요하다.

단어를 dense representation으로 만드는 방법을 word embedding이라고 하며 그 결과로 나오는 dense vector를 embedding vector(임베딩 벡터)라고도 부른다. 본 글에서는 embedding vector를 만드는 여러가지 방법 중 Word2Vec에 대해 알아본다.

2. Word2Vec

Word2Vec은 임베딩 벡터 사이에 유사도를 계산하여 확률로 변경한다.

• 유사도가 높을수록 확률이 높다. 반대로, 낮을수록 확률이 낮다.

문장 내에서 같이 등장하는 단어일수록 확률을 높이는 방식으로 학습한다.

• ‘마신다’라는 단어는 ‘물’과 같은 단어와 같이 등장한다. ‘마신다’라는 단어는 거의 상관이 없는 ‘건물’ 임베딩 벡터와의 유사도보다 ‘물’ 임베딩 벡터와의 유사도가 더 높을 것이다.
• ‘마신다’ 임베딩 벡터와 ‘물’ 임베딩 벡터사이의 유사도 > ‘건물’이라는 임베딩 벡터와의 유사도

Word2Vec의 종류

Word2Vec은 supervised learning 방식을 이용해 학습한다. 앞서 한 단어에 대해 문장 내에서 같이 등장하는 단어들을 표시한다고 했다. 이 때 한 단어를 중심 단어(center word)라고 하고 문장 내에서 같이 등장하는 단어를 주변 단어(context word)라고 한다.

Word2Vec은 2가지 학습 방법으로 나뉜다.

• CBOW: 주변 단어를 통해 중심 단어를 예측하는 방법
• Skip-Gram: 중심 단어를 통해 주변 단어를 예측하는 방법

일반적으로 Skip-Gram이 CBOW보다 성능이 좋다고 알려져있다. Skip-Gram은 중심 단어를 이용하여 주변 단어를 예측하기 때문에 하나의 단어가 여러 문맥을 고려하기 때문이다. (여러 단어를 예측하기 때문에 다양한 방면을 모두 고려한다) 반대로 CBOW는 주변 단어를 이용해 중심 단어를 예측하기 때문에 하나의 단어가 여러 문맥을 고려하기 어렵다.

CBOW나 Skip-Gram이나 방식의 차이는 있지만 네트워크 구조는 동일하기 때문에 각 방식을 이해하고 모델을 구성하는데 큰 어려움은 없을 것 같다.

3. Word2Vec 알고리즘의 원리

중심 단어, 주변 단어 데이터 셋 구성하기

이해를 위해 간단한 예시를 통해 설명하도록 하겠다.

• 예시: “I study math at school”
• vocab: [I, study, math, at, school]
• 문장에서 각 위치를 id라고 가정한다.

주변 단어를 선택하기 위해서 중심 단어를 기준으로 앞 뒤로 몇 개의 단어를 선택할 것인지 결정해야한다. 선택의 범위를 윈도우(window)라고 한다. 윈도우 크기가 2이라고 가정해보자.

• 중심 단어: I → 주변 단어: / study, math
• 중심 단어: study → 주변 단어: I / math, at
• 중심 단어: math → 주변 단어: I, study / at, school
• 중심 단어: at → 주변 단어: study, math / school
• 중심 단어 school → 주변 단어: math, school /

중심 단어를 기준으로 좌∙우로 윈도우 크기만큼의 단어가 주변 단어로 포함되는 것을 알 수 있다.

중심 단어가 옆으로 바뀌면서 윈도우가 같이 옆으로 이동되는 것을 확인할 수 있는데 이러한 방식을 슬라이딩 윈도우(sliding window)라고 한다.

모델의 학습을 위해 각 중심 단어와 주변 단어를 one-hot vector로 변경한 후 데이터셋을 구성한다.

(Word2Vec 알고리즘을 설명하기 위한 기본 데이터셋)

주변 단어(입력)	중심 단어(예측)	모델 입력	ground-truth
study	I	[0,1,0,0,0]	[1,0,0,0,0]
math	I	[0,0,1,0,0]	[1,0,0,0,0]
I	study	[1,0,0,0,0]	[0,1,0,0,0]
math	study	[0,0,1,0,0]	[0,1,0,0,0]
at	study	[0,0,0,1,0]	[0,1,0,0,0]

입력 데이터와 ground-truth를 통해서 CBOW는 입력 벡터와 출력 벡터가 동일한 차원임을 알 수 있다.

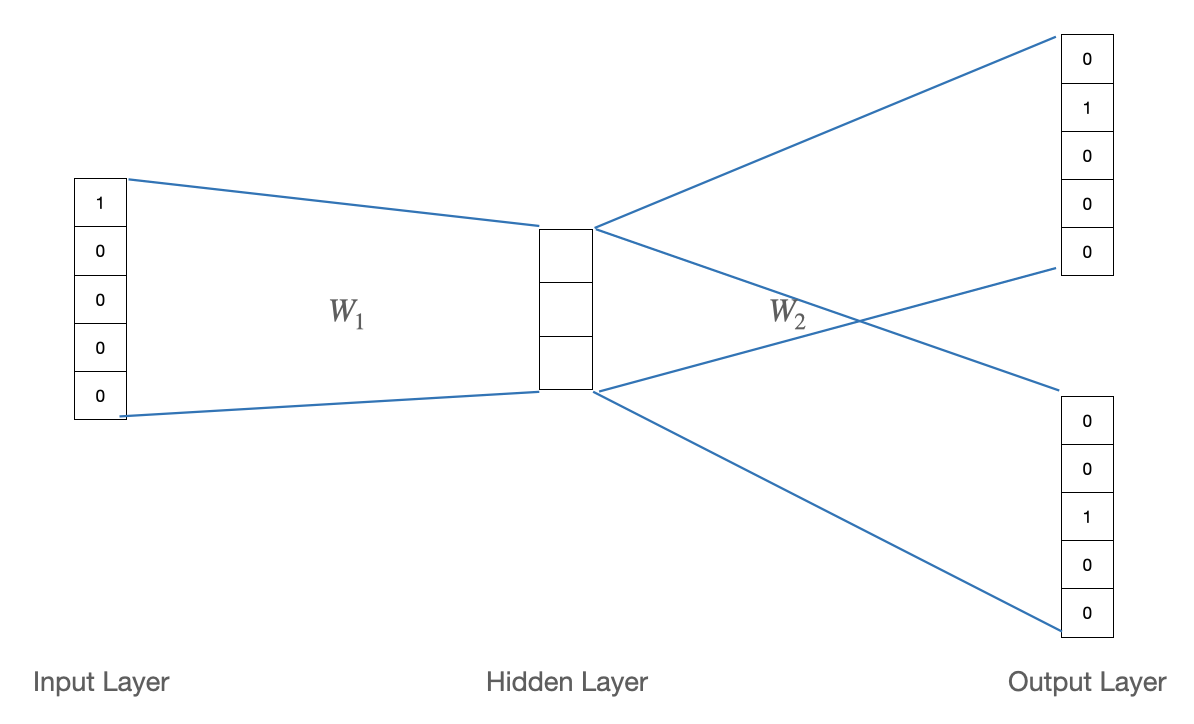
Word2Vec 모델의 기본 구조

기본적으로 Word2Vec은 2개의 선형 변환 layer로 이루어진 구조이며 activiation function을 사용하지 않는다.

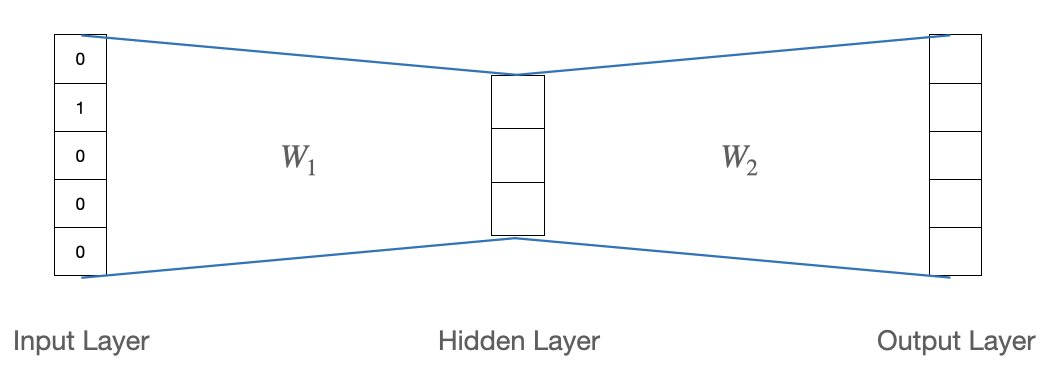
• 첫번째 층의 가중치: $W_1: 5 \times 3$ 행렬
• 두번째 층의 가중치: $W_2: 3 \times 5$ 행렬
• $\hat{y} = W_2W_1x$ ( $x,y \in \mathbb{R}^5$ )

첫번째 층에서 일어나는 연산을 살펴보자.

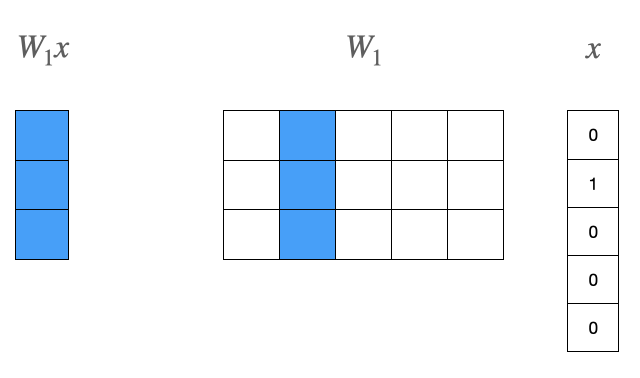
• $W_1x$는 결과적으로 $W_1$의 2번째 열벡터를 그대로 가져오게된다.
  • 입력으로 들어오는 $x$는 vocab의 2번째 단어인 study를 가리킨다.
  • 2번째 단어인 study의 one-hot vector와 곱해져 $W_1$의 2번째 열벡터를 오게 되었다.(lookup)

두번째 층에서 일어나는 연산을 살펴보자.

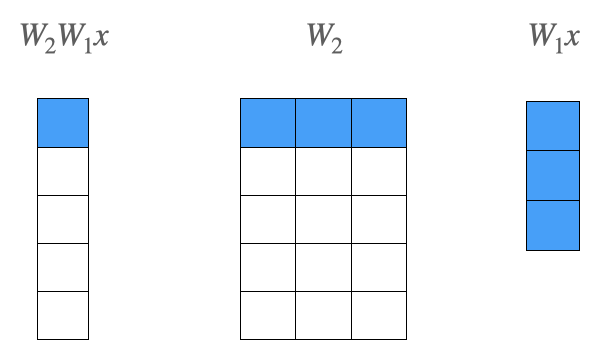
• $W_1$의 2번째 열벡터와 $W_2$의 행벡터의 내적 값이 출력 벡터의 원소가 된다.
• $W_2$의 첫번째 행벡터와 출력벡터의 첫번째 원소를 파랗게 색칠한 이유는 해당 원소가 ground-truth와 비교되기 때문이다.

두번째 층까지의 결과와 ground-truth간의 cross-entropy loss를 계산한 결과를 바탕으로 CBOW 모델을 학습한다. multi-class classification 문제로 풀 수 있다.

• $W_1$의 2번째 열벡터와 $W_2$의 첫번째 행벡터의 내적값이 가장 커지도록 학습이 된다.

$W_1$, $W_2$의 의미

Word2Vec을 통해 단어의 임베딩 벡터를 만든다고 했다. 그렇다면 Word2Vec의 어떤 부분이 임베딩 벡터가 될 수 있을까?

$W_1$의 열벡터와 $W_2$의 행벡터가 Word2Vec으로 구한 임베딩 벡터가 될 수 있다. $W_1$의 열과, $W_2$의 행은 모두 5로 단어 집합의 크기와 동일하기때문이다. 이 때 임베딩 벡터의 차원은 3이 된다.

• $W_1$의 2번째 열벡터는 study의 임베딩 벡터가 된다. 마찬가지로 3번째 열벡터는 math의 임베딩 벡터가 된다.
  • 앞서 $W_1x$의 결과가 $W_1$의 2번째 열벡터를 그대로 가져오게되는(lookup) 것과 동일하다고 언급하였다. 이는 결국 2번째 단어인 study의 임베딩 벡터를 가져온 결과라고 할 수 있다.
• $W_1$의 2번째 행벡터는 study의 임베딩 벡터가 된다. 마찬가지로 3번째 행벡터는 math의 임베딩 벡터가 된다.
  • 앞서 $W_1$의 2번째 열벡터와 $W_2$의 1번째 행벡터의 내적값이 가장 커지도록 학습이 된다고 언급하였다. 이는 결국 2번째 단어인 study의 임베딩 벡터($W_1$의 2번째 열벡터)와 1번째 단어인 I의 임베딩벡터($W_2$의 1번째 행벡터)사이의 내적값이 가장 커지도록 학습이 되는 것이다.

보통 $W_1$,$W_2$ 중 하나를 선택해서 임베딩 벡터로 사용한다.

4. CBOW 모델

CBOW는 주변 단어를 통해 중심 단어를 예측하는 형태로 학습하는 모델이다. 따라서 데이터셋의 구성이 다음과 같은 형태로 이루어진다.

주변 단어(입력)	중심 단어(예측)	모델 입력	ground-truth
study, math	I	[0,1,0,0,0], [0,0,1,0,0]	[1,0,0,0,0]
I, math, at	study	[1,0,0,0,0], [0,0,1,0,0], [0,0,0,1,0]	[0,1,0,0,0]

구조는 Word2Vec의 기본 구조와 동일하다. 하지만 입력에서 one-hot vector를 동시에 여러개를 받기 때문에 첫번째 층을 통과한 후 입력으로 들어오는 벡터의 갯수만큼 벡터가 나오게된다. CBOW는 첫번째 층의 결과로 나오는 벡터들을 평균내어 하나의 벡터로 만든 후 두번째 층의 입력으로 사용한다.

• 첫번째 데이터를 사용하게되면 $W_1$의 2번째 열벡터와 3번째 열벡터가 첫번째 층의 결과로 나온다. 이 벡터들을 평균 내어 두번째 층의 입력으로 사용하게 된다.

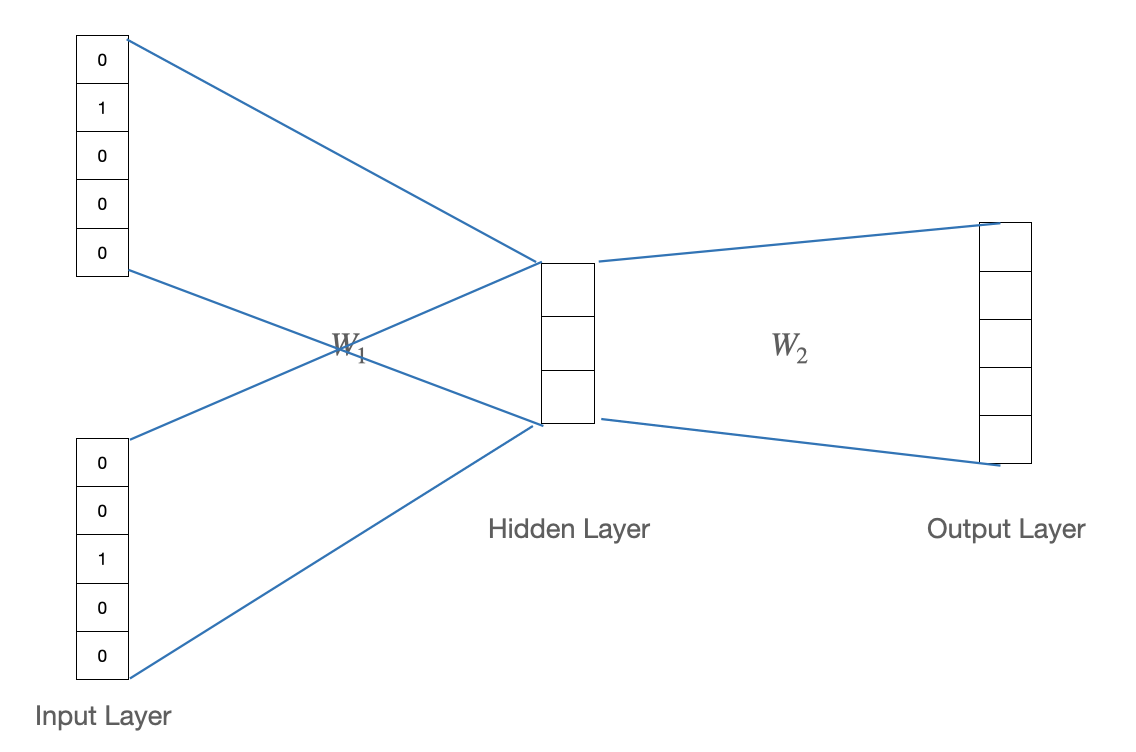
5. Skip-Gram 모델

Skip-Gram은 중심 단어를 통해 주변 단어를 예측하는 형태로 학습하는 모델이다. 따라서 다음과 같은 형태로 데이터셋을 구성한다.

중심 단어(입력)	주변 단어(예측)	모델 입력	ground-truth
I	study, math	[1,0,0,0,0]	[0,1,0,0,0], [0,0,1,0,0]
study	I, math, at	[0,1,0,0,0]	[1,0,0,0,0], [0,0,1,0,0], [0,0,0,1,0]

CBOW와 달리 모델의 입력으로 벡터 1개가 들어오기 때문에 평균을 내는 과정은 없다. 대신 ground-truth가 여러개이기 때문에 각 벡터에 대해 cross-entropy loss를 계산한 후 모두 더한 것이 입력 데이터에 대한 최종 loss가 된다.(실제로 구현된 것을 참고했을 때 평균을 내어 사용하는 경우도 있는 것 같다.)