[NLP] Transformer와 Self-Attention
Updated:
1. Attention is All You Need
RNN 계열 모델의 단점
- 한정된 차원의 벡터에 source sequence(input sequence)의 모든 정보를 담기 때문에 정보를 모두 기억하지 못하고 유실할 수도 있다.
- Long-term dependency 문제
- gradient vanishing 현상으로 인해 학습이 제대로 이루어지지 않는다.
- 순차적으로 학습하기 때문에 학습 속도가 느리다. (병렬 연산이 불가능하다.)
Attention is All You Need
해당 논문은 Transformer라는 새로운 모델을 제시하였다. seq2seq 모델의 Encoder∙Decoder 구조를 사용하고 있으며 내부의 RNN 모듈을 Attention 모듈로 모두 대체하였다.
- long-term dependency 문제를 해결하였다.
- 병렬 연산이 가능해져 모델의 학습 속도를 올린다.
Transformer 이후로 나오는 pre-trained 모델 대다수가 Transformer의 Encoder 혹은 Decoder를 응용하거나 단순히 층을 깊게 쌓은 형태로 성능을 끌어올렸다.
2. Scaled Dot-Product Attention (Self-Attention)
Encoder 내부에 존재하는 RNN을 없애기 위해 Self-Attention이라는 새로운 형태의 Attention을 사용하였다.
Self-Attention은 self라는 이름에서 알 수 있듯이 자기 자신만을 사용하여 Attention 계산을 진행한다.
Query, Key, Values
seq2seq with attention에 적용된 attention 과정을 되짚어 보면 다음과 같다.
- decoder hidden state vector와 encoder hidden state vectors 간의 내적을 통해 attention-score를 계산한다.
- 계산된 attention-score를 softmax 함수를 이용하여 attention distribution을 계산한다.
- attention distribution을 가중치로 사용하여 encoder hidden state vectors 의 가중합 벡터를 구한다.
Attention 과정을 살펴보면 총 3가지 형태의 벡터가 필요한 것을 알 수 있다.
- 내적 연산을 위해 2가지 벡터가 필요하다.
- 유사도 계산을 하려는 벡터 → decoder hidden state vector
- 유사도를 구하기 위한 대상이 되는 벡터 → encoder hidden state vectors
- 계산된 attention distribution을 이용해 가중합을 구할 수 있는 벡터가 필요하다. → encoder hidden state vectors
Self-Attention에서 각각의 역할을 하는 벡터를 query, key, value라고 부른다.
- 유사도 계산을 하려는 벡터: query 벡터
- 유사도를 구하기 위한 대상이 되는 벡터: key 벡터
- 마지막으로 가중합되는 벡터: value 벡터
Self-Attention은 앞서 언급했듯이 attention을 자기 자신에게 수행하기 때문에 각각의 벡터들을 하나의 sequence 안에서 모두 만들어야한다.
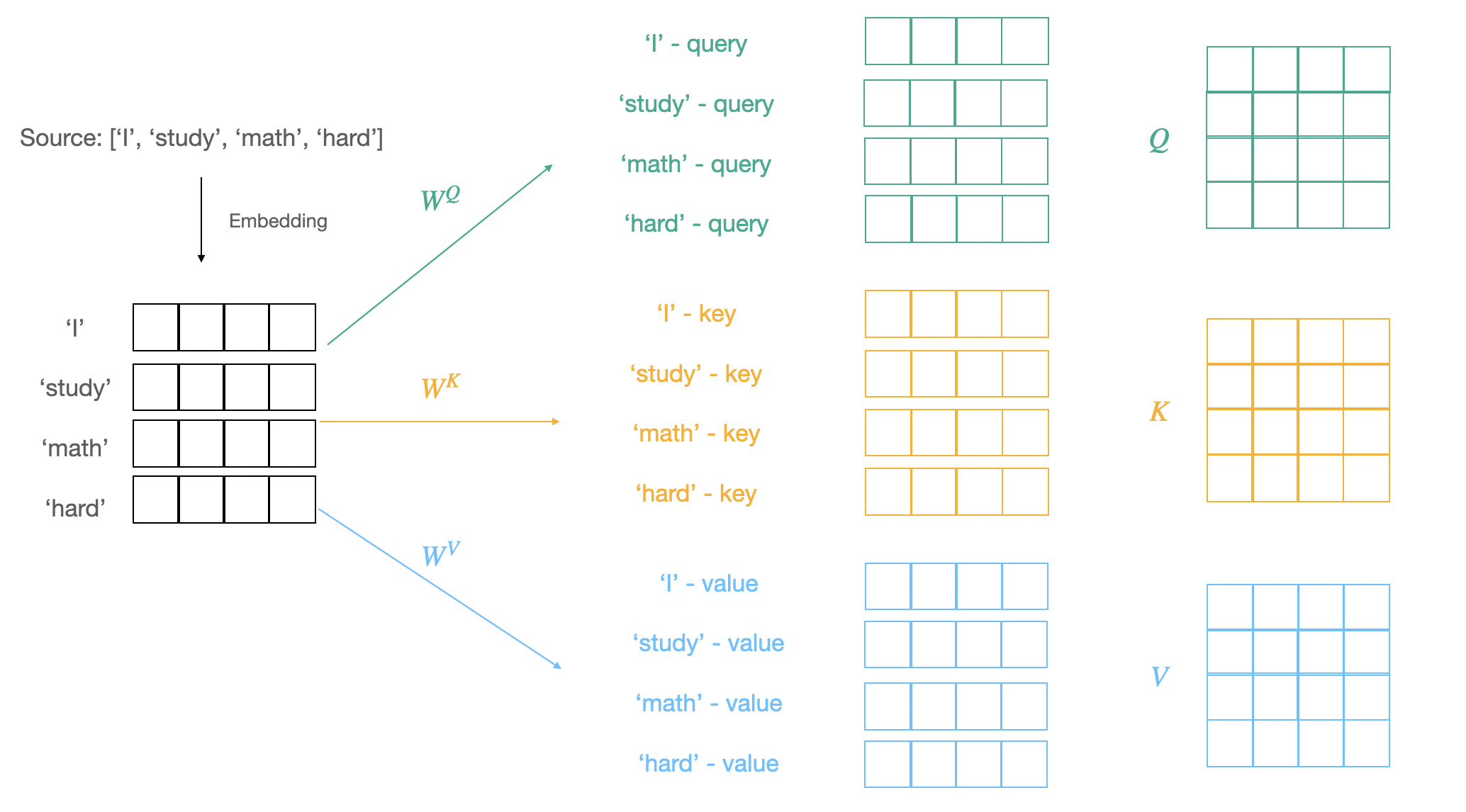
따라서 선형 변환을 이용해 query, key, value로 변환하는 과정을 거친다.
- $W^Q$, $W^K$,$W^V$라는 가중치 행렬을 이용하여 선형 변환을 통해 query, key, value 벡터로 만든다.
- query: $W^Q$를 이용하여 선형변환을 진행한다. → $d_k$ 차원의 벡터
- key: $W^K$를 이용하여 선형변환을 진행한다. → $d_k$ 차원의 벡터
- value: $W^V$를 이용하여 선형변환을 진행한다. → $d_v$ 차원의 벡터
Dot-Product Attention
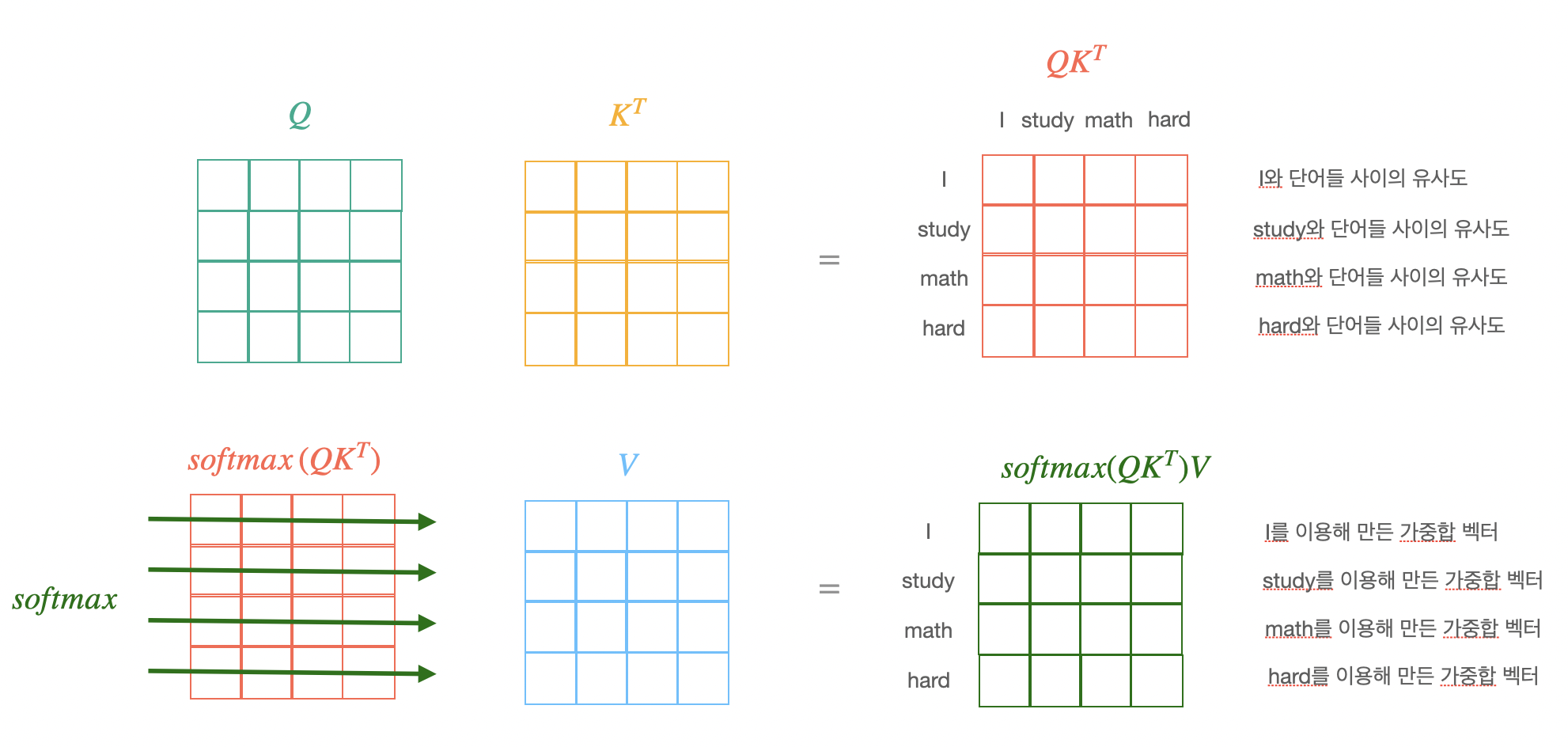
만들어진 query, key, value 벡터를 이용하여 dot product attention을 진행한다.
$A(q,K,V) = \sum\limits_i \frac{exp(q \cdot k_i)}{\sum_j exp(q \cdot k_j)} v_i$
- $q$: query vector
- $K$: key matrix
- $V$: value matrix
query를 stack으로 쌓아 하나의 행렬로 만들면 식이 다음과 같이 바뀌어 계산이 더 편해진다.
$A(Q,K,V) = softmax(QK^T)V$
- softmax연산은 row-wise로 실행한다
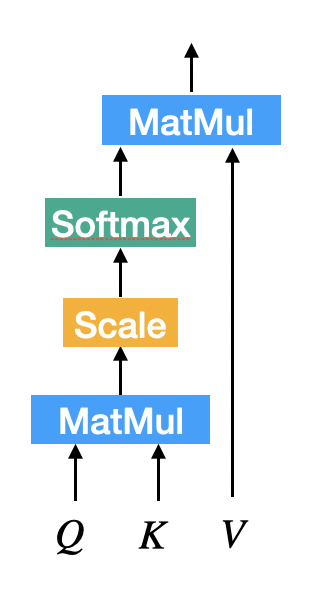
Scaled Dot-Product Attention
$A(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$
- Dot-Product Attention을 $\sqrt{d_k}$만큼 scailing함
3. Multi-Head Attention
Self-Attention을 1번만 사용할 때의 단점
각 단어들이 서로 한 가지 방법으로만 상호작용한다는 단점이 존재한다.
- 문장 내에서 각 단어가 가지는 여러가지 의미를 파악할 수 없다.
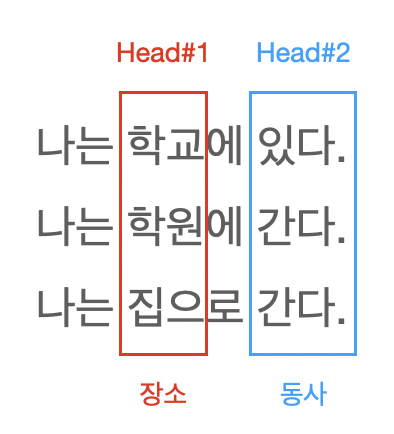
Multi-Head Attention
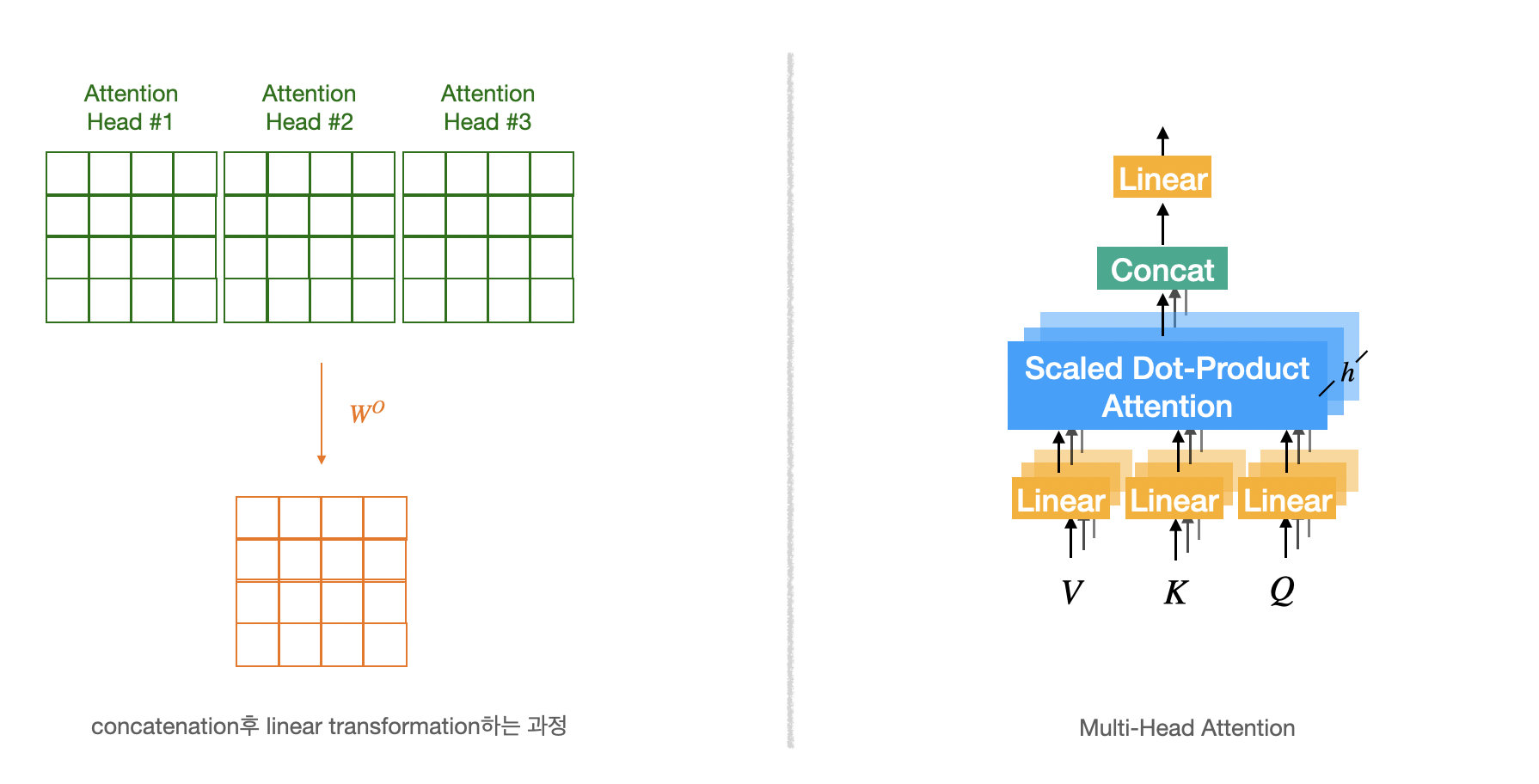
Multi-Head Attention은 Scaled Dot-Product Attention을 $h$번 수행하는 것을 뜻한다.
$MultiHead(Q,K,V) = concat(head_1,\dots,head_h)W^O$
$where \, head_i = Attention(QW_i^Q,KW_i^K,VW_i^V)$
- Scaled Dot-Product Attention을 $h$번 수행한 뒤 나오는 $h$개의 행렬을 모두 concatenation한다.
- Scaled Dot-Product Attention마다 사용되는 가중치 행렬($W_i^Q$,$W_i^K$,$W_i^V$)이 모두 다르기 때문에 Query, Key, Value 행렬 또한 모두 다르다.
- concatenation되어 늘어난 차원을 다시 원래 차원(dimension)으로 변경해주기위해 $W^O$ 가중치 행렬을 이용하여 선형변환한다.
4. Encoder
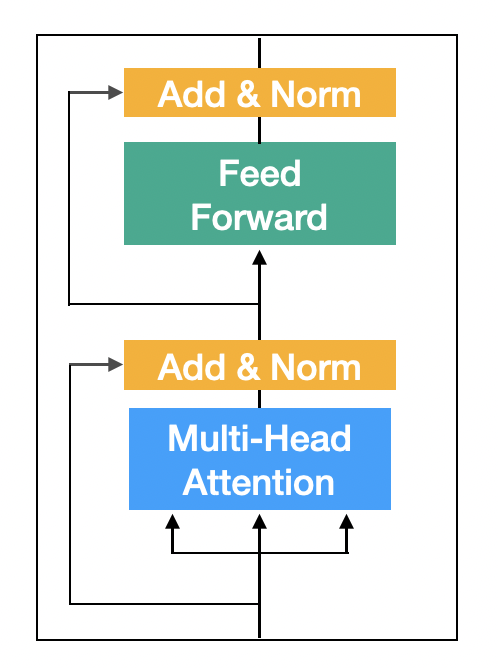
Encoder Block 구성하기
Encoder Block은 2개의 sub-layer로 구성이되어있다.
- Multi-Head Attention
- ReLU를 사용하는 2-Layer Feed Forward Neural Network
sub-layer마다 Residual Connection과 Layer Normalization이 적용된다.
- $LayerNorm(x+sublayer(x))$
- Residual Connection을 사용하기 때문에 sub-layer의 출력과 입력의 차원(dimension)이 동일해야한다.
Positional Encoding
Attention을 할 때마다 입력 순서에 상관없이 행렬곱을 하기 때문에 sequence의 순서 정보가 사라진다.
- [I, go, home]과 [home, go, I]의 attention 결과로 나오는 가중합 벡터가 동일하다.
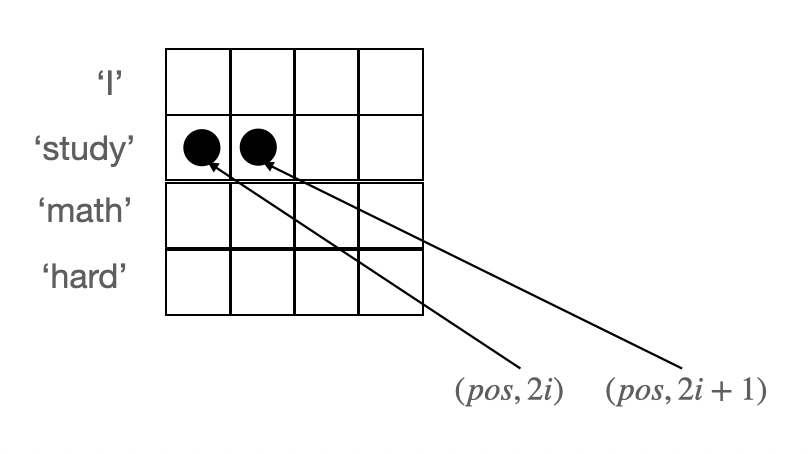
각 차원(dimension)마다 일정한 상수를 더해줌으로써 입력 순서를 구분할 수있게 해주는 방법이 Positional Encoding이다.
$PE_{(pos,2i)} = sin(pos/10000^{2i/d_{model}})$
$PE_{(pos,2i+1)} = cos(pos/10000^{2i/d_{model}})$
- $pos$: sequence에서 몇번째 위치인지 나태나는 값
- $i$: dimension을 가리킨다.
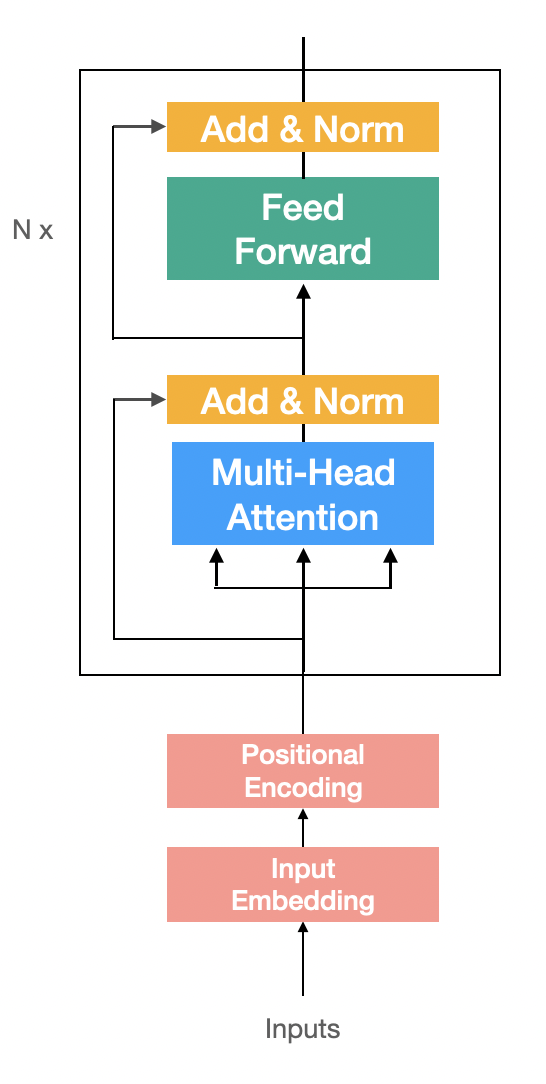
Encoder
input을 받아 Embedding과 Postional Encoding 작업을 해준뒤 N개의 Encoder Block을 쌓아 만든다.
5. Decoder
Masked Multi-Head Attention
Decoder에서는 다음 단어를 예측하는 작업이 이루어지기 때문에 Attention 과정에서 예측해야할 단어들을 보지 못하도록 masking 처리를 해주어야한다.
Attention score를 계산한 이후 예측해야할 단어들에 해당하는 부분을 masking처리를 해준다.
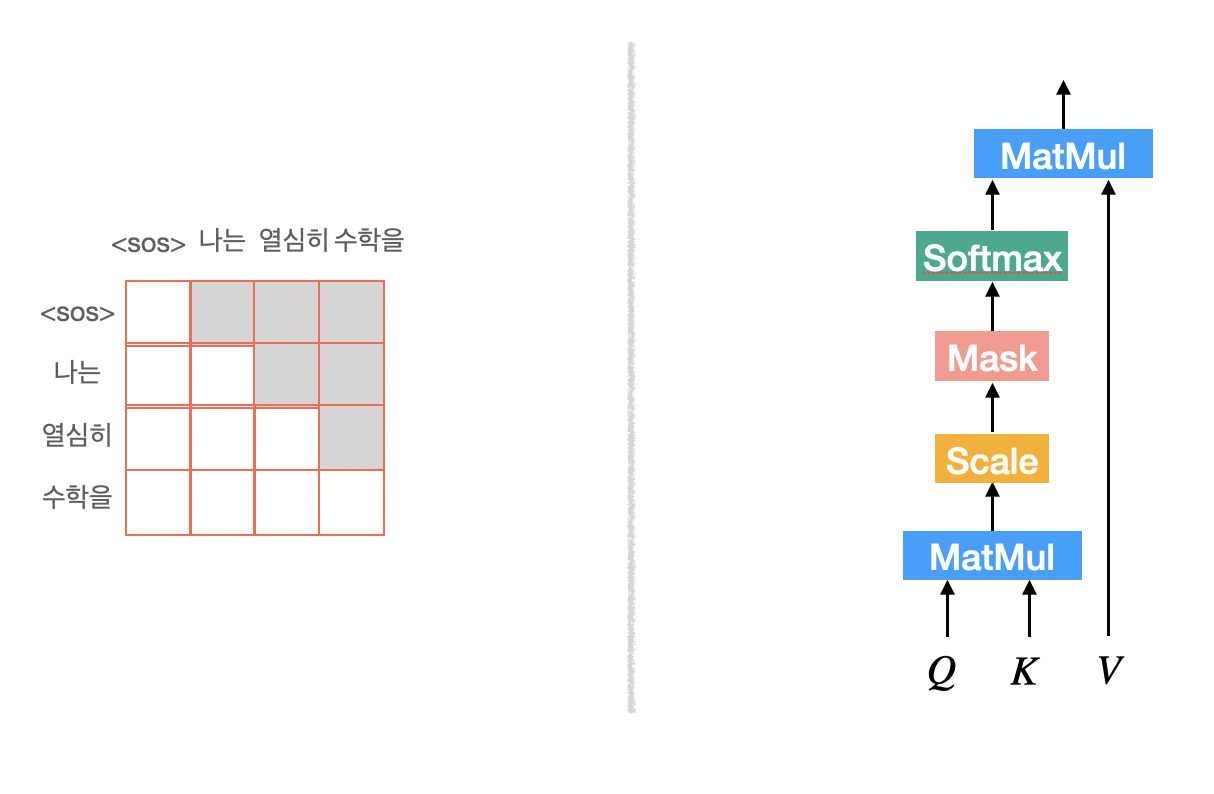
나머지 과정은 Multi-Head Attention과 동일하다.
Multi-Head Attention (Encoder-Decoder Attention)
Decoder에서 특별한 형태의 Multi-Head Attention이 하나 더 사용되는데 Encoder-Decoder Attention이다.
형태는 Multi-Head Attention이지만 Self-Attention이 아니다. 더 구체적으로 설명하면 query는 자기 자신을 이용해 만들지만 key와 value는 Encoder의 출력을 사용한다.
- source sequence의 정보를 이용해 target sequence를 예측하기 때문에 key와 value는 Encoder의 출력을 사용한다.
- 마치 seq2seq with attention 모델에서 decoder의 hidden state vector와 encoder의 hidden state vectors간의 Attention을 수행하는 과정처럼 보면 될 것 같다.
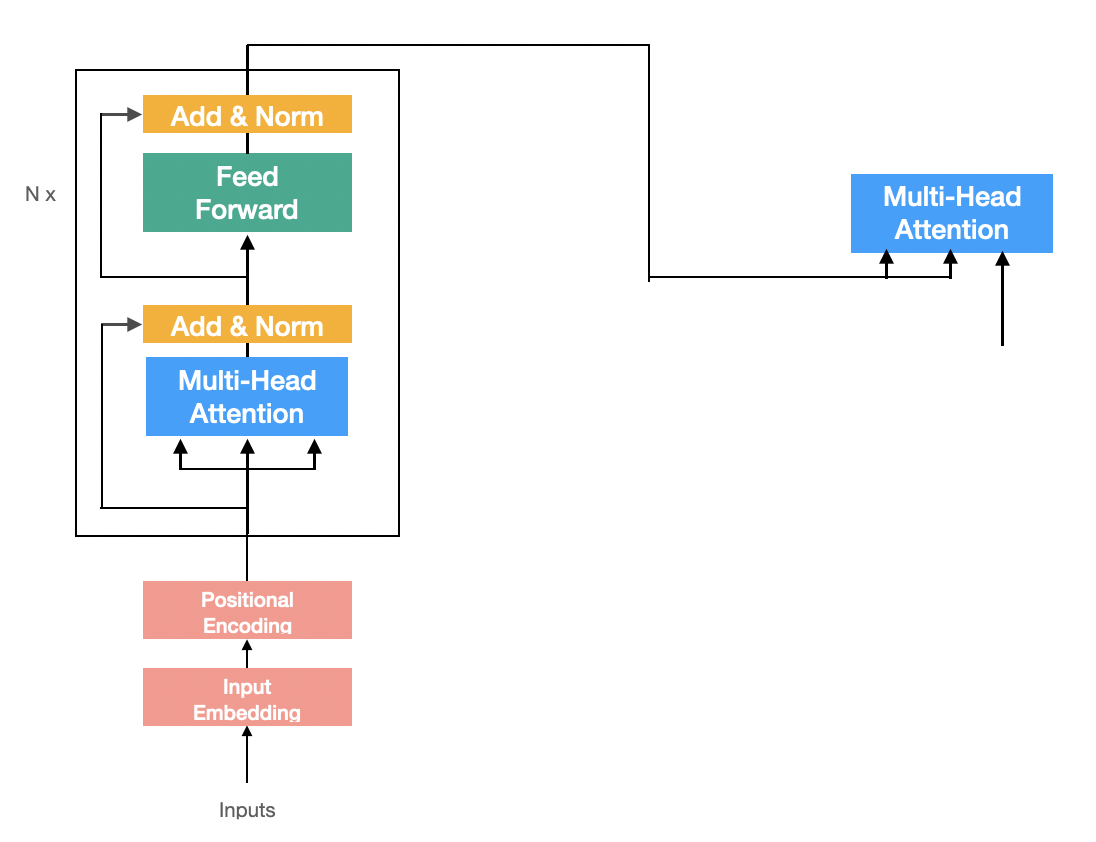
Input & Positional Encoding
Decoder에서는 다음 단어를 예측하면서 문장을 생성한다. 따라서 sequence의 시작 부분에
- 나는 열심히 수학을 공부한다 →
나는 열심히 수학을 - sequence가 오른쪽으로 하나씩 밀렸다고 해서 shifted right 형태라고 한다.
하나씩 밀리기 때문에 마지막 단어는 input으로 들어가지 않게된다.
이후 Encoder에 적용된 Positional Encoding을 Decoder에도 적용한다.
Decoder Block
Decoder Block은 총 3개의 sub-layer로 구성되어있다.
- Masked Multi-Head Attention
- Multi-Head Attention(Encoder-Decoder Attention)
- ReLU를 사용한 2-layer Feed Forward Neural Network
sub-layer 마다 Residual Connection과 Layer Normalization이 적용된다.
- $LayerNorm(x+sublayer(x))$
- Residual Connection을 사용하기 때문에 sub-layer의 출력과 입력의 차원(dimension)이 동일해야한다.
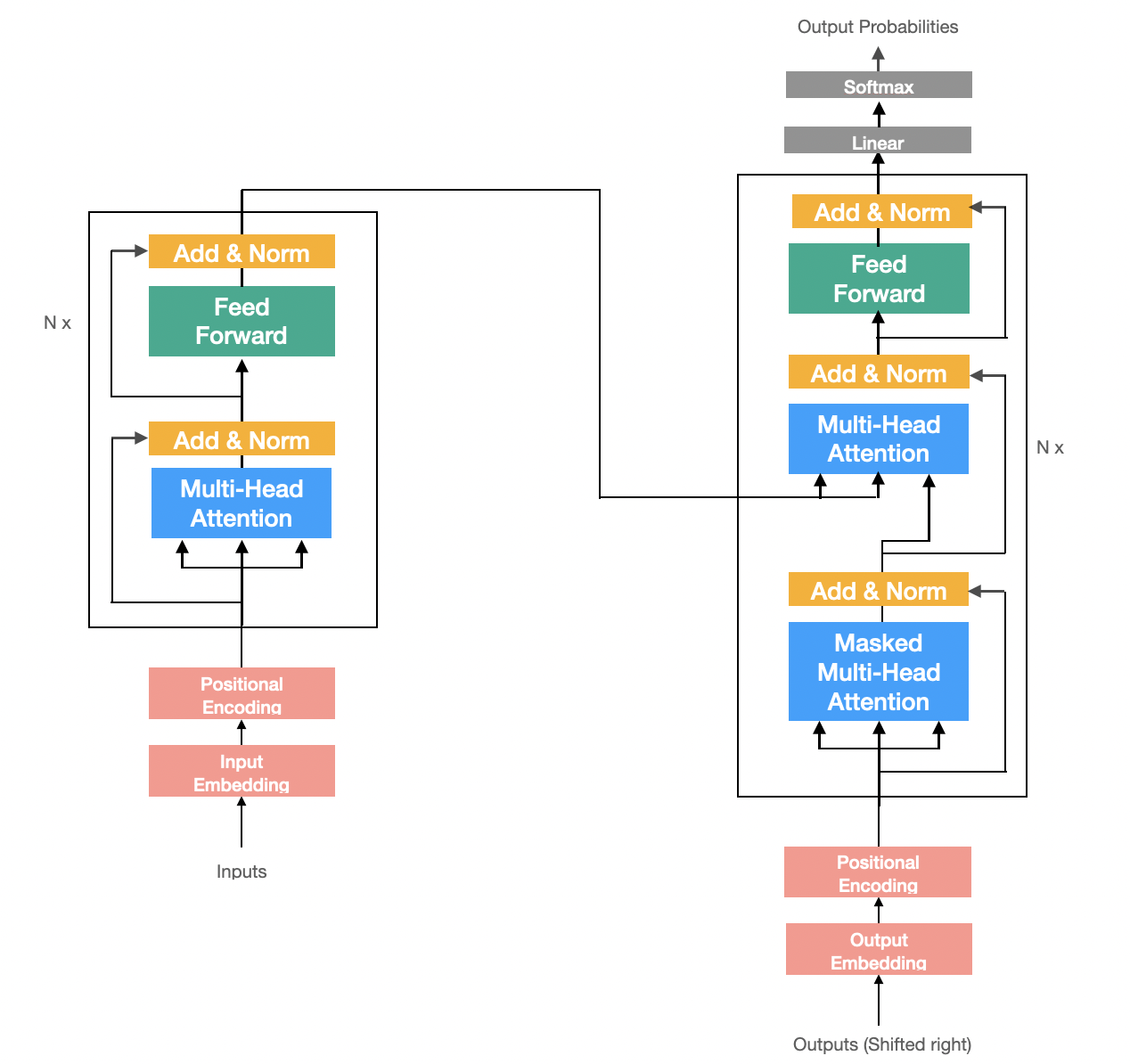
Decoder
Embedding과 Postional Encoding 작업을 해준뒤 N개의 Decoder Block을 쌓아 만든다.
다음 단어를 예측하기 위해 Decoder Block이후 linear transformation과 softmax를 사용해 multi-class classification 문제를 푼다.
- linear transformation: Decoder Block 출력값의 차원을 vocab size로 변경하는 역할을 한다.
Leave a comment